The Wordle craze has inspired many clones, including Worldle. In this version, you are shown an outline of a country or territory (including uninhabited islands) and have six guesses to figure out which country or territory is displayed. With each incorrect guess you are told how far the center of the country you guessed is from the center of the correct country in kilometers, as well as the general direction.
When playing the other day, I had this outline and did not even have a clue about what country it could be.
So I started with some random guesses, hoping I could narrow it down by rudimentary triangulation. After three guesses I had the following results.
guesses <- tibble::tribble(
~Country, ~Distance, ~Direction,
'Iceland', 13427, 'South',
'Sierra Leone', 7144, 'South',
'Lesotho', 3404, 'Southwest'
)
guesses| Country | Distance | Direction |
|---|---|---|
| Iceland | 13427 | South |
| Sierra Leone | 7144 | South |
| Lesotho | 3404 | Southwest |
The best I could tell was that the correct answer was somewhere in the middle of the South Atlantic Ocean but it was probably a small island that would be hard to find by panning through Google Maps. So I decided to use R and the {sf} package to help locate the correct answer.
The goal with the code is to find the centers of each guess, draw circles around those centers, each with a radius as given by the distance in the game, then see where the three circles intersect. This is the general idea behind triangulation and should show us roughly where the correct country is positioned.
First, I needed to find the centers of my incorrect guesses, so I used the {rnaturalearth} package to pull up the boundaries of the countries guessed so far and then use st_centroid() to compute their centroids.
library(sf)
library(dplyr)
data(countries110, package='rnaturalearth')
# this is an sp object so we make it into sf
countries <- countries110 |> st_as_sf()
# here we narrow it down to the countries we want to keep
starting <- countries |>
select(brk_name) |>
inner_join(guesses, by=c('brk_name'='Country')) |>
# leaflet makes you assign your own colors
mutate(color=RColorBrewer::brewer.pal(n(), 'Set1'))
# this finds the centroids of each country
# the warning doesn't apply to us
centers <- starting |>
st_make_valid() |>
st_centroid()## Warning in st_centroid.sf(st_make_valid(starting)): st_centroid assumes
## attributes are constant over geometries of x# these are the centers of each guess
centers| brk_name | Distance | Direction | geometry | color |
|---|---|---|---|---|
| Iceland | 13427 | South | POINT (-18.76554 65.07986) | #E41A1C |
| Lesotho | 3404 | Southwest | POINT (28.17182 -29.62479) | #377EB8 |
| Sierra Leone | 7144 | South | POINT (-11.79541 8.529459) | #4DAF4A |
Now we map these points to see how we’re doing. For this blog, the maps are static though when recreating this in the console or an HTML rmarkdown document, they would be pannable and zoomable.
library(leaflet)
leaflet() |>
addTiles() |>
# we use the color column defined earlier
addPolygons(data=starting, fillColor=~color, stroke=FALSE, opacity=1) |>
addMarkers(data=centers)
For each of our guesses, we want to draw a circle extending out from their centers. The radius of each circle is given by the distance reported in the game. To compute these circles we use st_buffer() which creates a polygon around a given geometry, the points in this case.
The latest version of {sf} uses spherical geometry by default. This means we can pass an sf object that uses lat/long to st_buffer(), specifying the dist argument in kilometers, and st_buffer() will account for the curvature of the Earth. In previous versions, we would first convert to a meters-based projection (which is hard to do on a global scale) then compute the buffer then convert back to lat/long. Spherical geometry is a huge improvement.
st_buffer() returns the entire circle as a filled in polygon, but we actually just want the boundaries of the circles because we want to compute the intersection of the boundaries not of the insides of the circles. To convert our circle polygons to just the outlines we use st_cast("LINESTRING").
circles <- centers |>
# we use the distance from each center
# this is stored in km so we multiply by 1000 to get meters
st_buffer(dist=centers$Distance*1000) |>
# get just the outline of the cirles
st_cast("LINESTRING")## Warning in st_cast.sf(st_buffer(centers, dist = centers$Distance * 1000), :
## repeating attributes for all sub-geometries for which they may not be constantleaflet() |>
addTiles() |>
# we use the color column defined earlier
addPolylines(data=circles, color=~color, popup=~brk_name) |>
addMarkers(data=centers)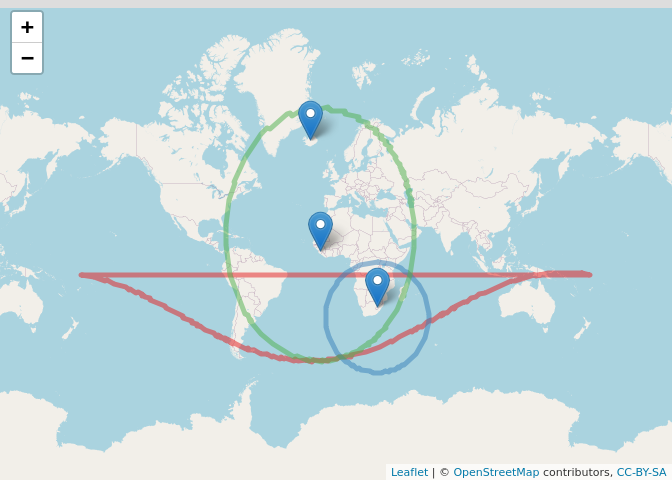
The circle for Iceland, in red, is only displayed as a semicircle. This is due to its radius being so large and extending over the north pole. Fortunately, that doesn’t matter for our purposes. By looking where the three circles intersect we should be able to find the country we are searching for.
With triangulation, the three circles will intersect in just one spot. It may appear that all three circles intersect in two places, but this is an artifact of the circle around Iceland being weirdly displayed.
To find where all the circles intersect we find any intersection amongst them with st_intersection() then narrow down the resulting points to those that have three or more overlaps.
overlaps <- circles |>
st_intersection() |>
filter(n.overlaps >= 3)
overlaps| brk_name | Distance | Direction | color | n.overlaps | origins | geometry | |
|---|---|---|---|---|---|---|---|
| 1.2 | Iceland | 13427 | South | #E41A1C | 3 | 1, 2, 3 | POINT (3.483787 -54.73521) |
This means we should focus our search at (3.4838,-54.7352). Since the measurements are not exact we look for this point on a map plus a little extra to help us see what’s around it.
leaflet() |>
addTiles() |>
addCircles(data=overlaps) |>
# 100 km search area
addPolylines(data=overlaps |> st_buffer(dist=100*1000))And we found Bouvet Island! This little uninhabited nature reserve isn’t even in the data.frame provided by {rnaturalearth} so I’m not sure how I would have found it without {sf}.
Spatial analytics and GIS are a really powerful part of data science and I have been using them more and more for clients lately. I’ve also given a couple talks recently where you can see more about GIS.
While Worldle is fun to play on its own, it was even more fun using R to find the solution for a particularly tricky problem.

Jared Lander is the Chief Data Scientist of Lander Analytics a New York data science firm, Adjunct Professor at Columbia University, Organizer of the New York Open Statistical Programming meetup and the New York and Washington DC R Conferences and author of R for Everyone.

