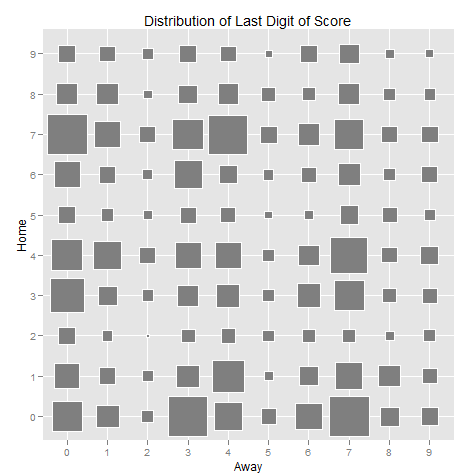
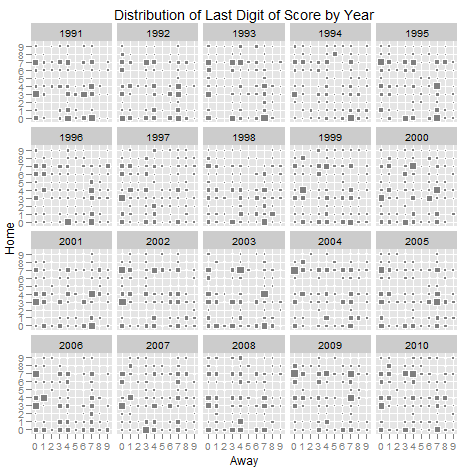
Shortly after the Giants fantastic defeat of the Patriots in Super Bowl XLVI (I was a little disappointed that Eli, Coughlin and the Vince Lombardi Trophy all got off the parade route early and the views of City Hall were obstructed by construction trailers, but Steve Weatherford was awesome as always) a friend asked me to settle a debate amongst some people in a Super Bowl pool.
He writes:
We have 10 participants in a superbowl pool. The pool is a “pick the player who scores first” type pool. In a hat, there are 10 Giants players. Each participant picks 1 player out of the hat (in no particular order) until the hat is emptied. Then 10 Patriots players go in the hat and each participant picks again.
In the end, each of the 10 participants has 1 Giants player and 1 Patriots player. No one has any duplicate players as 10 different players from each team were selected. Pool looks as follows:
| Participant 1 |
Giant A |
Patriot Q |
| Participant 2 |
Giant B |
Patriot R |
| Participant 3 |
Giant C |
Patriot S |
| Participant 4 |
Giant D |
Patriot T |
| Participant 5 |
Giant E |
Patriot U |
| Participant 6 |
Giant F |
Patriot V |
| Participant 7 |
Giant G |
Patriot W |
| Participant 8 |
Giant H |
Patriot X |
| Participant 9 |
Giant I |
Patriot Y |
| Participant 10 |
Giant J |
Patriot Z |
Winners = First Player to score wins half the pot. First player to score in 2nd half wins the remaining half of the pot.
The question is, what are the odds that someone wins Both the 1st and 2nd half. Remember, the picks were random.
Before anyone asks about the safety, one of the slots was for Special Teams/Defense.
There are two probabilistic ways of thinking about this. Both hinge on the fact that whoever scores first in each half is both independent and not mutually exclusive.
First, let’s look at the two halves individually. In a given half any of 20 players can score first (10 from the Giants and 10 from the Patriots) and an individual participant can win with two of those. So a participant has a 2/20 = 1/10 chance of winning a half. Thus that participant has a (1/10) * (1/10) = 1/100 chance of winning both halves. Since there are 10 participants there is an overall probability of 10 * (1/100) = 1/10 of any single participant winning both halves.
The other way is to think a little more combinatorically. There are 20 * 20 = 400 different combinations of players scoring first in each half. A participant has two players which are each valid for each half giving them four of the possible combinations leading to a 4 / 400 = 1/100 probability that a single participant will win both halves. Again, there are 10 participants giving an overall 10% chance of any one participant winning both halves.
Since both methods agreed I am pretty confidant in the results, but just in case I ran some simulations in R which you can find after the break.
Continue reading →


Jared Lander is the Chief Data Scientist of Lander Analytics a New York data science firm, Adjunct Professor at Columbia University, Organizer of the New York Open Statistical Programming meetup and the New York and Washington DC R Conferences and author of R for Everyone.